Kako centrirati točak bicikla? Kako napraviti dobar točak koji dugo traje? Koje žbice i felne su najbolje? To su neka od pitanja na koja sam odgovorio ovim člankom.
U posebnom članku preporučio sam alate za pravljenje točkova bicikala.
Za prikaz proizvoda koristiću Amazon affiliate linkove za kupovinu i zaraditi procenat od kvalifikovanih kupovina (zašto Bike Gremlin koristi Amazon affiliate).
Sadržaj:
- Uvod u pravljenje točkova za bicikl
- Izbor kvalitetnih komponenata
2.1. Nable
2.2. Felne
2.3. Žbice
2.4. Niple - Način šniranja (pletenja) žbica
3.1. Kako ukršteno pleteni točkovi prenose opterećenje
3.2. Optimalan broj ukrštanja
3.3. Kako radijalno pleteni točkovi prenose opterećenje - Značaj izbora optimalne dužine žbica
- Računanje optimalne dužine žbica
- Značaj ujednačenosti tenzije žbica
- Prihvatljive tolerancije pri pravljenju točka bicikla
7.1. Radijalna centriranost
7.2. Lateralna centriranost
7.3. Poravnatost felne
7.4. Prihvatljive tolerancije centriranosti, i ujednačenosti tenzije žbica - Izvori – toplo preporučeni
1. Uvod u pravljenje točkova za bicikl
Ovaj članak je zamišljen kao “matični”, vezano za pravljenje točkova bicikala. U njemu sam se trudio objasniti sve bitne stvari i pojmove. Ako želite naučiti praviti dobre točkove za bicikl, mislim da ga vredi pročitati od početka do kraja. Sadržaj barem 4 knjige i 20ak godina iskustva ovde su sažeti u nekoliko strana veličine A4 – najkraće što mogu, a da bude jasno i početnicima.
U drugom prelazu članka, vredi kliktati na linkovane članke, koji detaljno objašnjavaju određenije aspekte. Naravno, mogu se koristiti i kasnije, po potrebi.
Puno kraće, samo osnovno o načinu na koji točkovi bicikla nose opterećenje i šta je važno da bi bili dobri i izdržljivi (izbor kvalitetnih komponenata), pisao sam u članku: Točkovi bicikla – koliko žbica? Možda je najbolje ipak prvo pročitati taj članak, da se shvate osnove.
U poslednjem, 8. poglavlju, stavio sam linkove ka odličnim izvorima na ovu temu, kao i sa svojim video snimcima koji praktično demonstriraju ono o čemu ovde pišem. Meni lično je lakše i brže nešto naučiti kada prvo pročitam i vidim slike/grafike, ali svakako sam se trudio napraviti i praktičnu demonstraciju jer to zaokružuje celu priču.
Članak jeste dugačak, ali nadam se da će pomoći onima koje ovo zanima, jer sadrži sve potrebne detalje, a bez neke egzotike i preteranog udubljivanja koji su više primereni knjizi, nego članku.
2. Izbor kvalitetnih komponenata
Ako se menja samo felna, ili nabla, izbor je u izvesnoj meri “olakšan”, jer su mnoge stvari određene ostalim komponentama. Zato ću u ovom tekstu poći od pretpostavke da se nov točak pravi “od nule”.
Na engleskom sam napravio YouTube snimak u kojem objašnjavam vrste, kvalitet i izbor komponenata za pravljenje točka bicikla.
2.1. Nable
Počeo bih od izbora nable. U zavisnosti od toga da li je točak prednji, ili zadnji, da li je za drumski bicikl, ili za MTB, da li se želi disk kočnica – izbor nable će biti različit. Izbor nable zavisi i od rama – da li ram prihvata nable sa quick-release mehanizmom, ili traži punu osovinu.
Zatim, ako se radi o zadnjoj nabli, treba videti kolika je širina zadnjih dropova, pa tražiti odgovarajuću nablu. U posebnom članku pisao sam o standardnim širinama zadnje nable. Ovo će dodatno suziti izbor nable.
Još jedna stvar koju treba utvrditi je da li ram bicikla prihvata disk, ili “obične” kočnice (linkovani članak objašnjava prednosti i mane jednih u odnosu na druge). Pošto postoje nable za disk kočnice. One će raditi i sa “običnim” kočnicama, ali su (nepotrebno, ako se koriste “obične” kočnice) skuplje i teže.
Kod zadnjih nabli, nije sve jedno ni koliko zadnjih lančanika se koristi, pa čak ni koja marka menjača je u pitanju (Shimano, SRAM, ili Campagnolo). To sam objasnio u članku o kompatibilnosti zadnjih nabli.
U okviru svih ovih zadatih parametara, koji u najvećoj meri zavise od toga za kakav se bicikl točak pravi, ostaje da se izabere koliko žbica. Po pitanju lakog nabavljanja felni, a i izdržljivosti točka, preporučio bih da se ide sa 32, ili 36 žbica. Od izabranog broja rupa za žbice na nabli, naravno, zavisiće i to kakva felna se traži (za koliko žbica).
Ovde bih napomenuo i da postoje “egzotične” nable za “egzotične” žbice, koje često traže i egzotičnu felnu. Evo jednog primera:

Slika 1

Slika 2

Slika 3
2.2. Felne
Kod felni je važno da imaju isti broj žbica (tj. rupa za niple) kao i izabrana nabla (i obrnuto).
Mislim da su duplozidne aluminijumske felne među jačim, dugotrajnijim, a nisu previše ni skupe, ni teške.


2.3. Žbice
Ne preskupo, a dobro rešenje su standardne, savijene u laktu, čelične, prečnika 2 mm. Idealno je ako su tanjene na sredini na 1,8 mm.
Pri tome, žbice prečnika 2 mm, ali tanjene na 1,5 mm (ne 1,8) se previše uvijaju prilikom pravljenja točka i zatezanja, a ne donose neku prednost.
Uže žbice, prečnika 1,8 mm na krajevima, su nešto malo laganije, više aerodinamične, ali manje dugotrajne. Neke od ovih žbica prave se da budu na sredini stanjene na 1,5 mm. Za razliku od širih žbica, od 2 mm, tanjenih na 1,5 mm na sredini, u ovom slučaju to ne otežava pravljenje točka previše, a donosi izvesnu prednost po pitanju dugotrajnosti. I dalje su žbice prečnika 2 mm na krajevima, a tanjene na 1,8 mm na sredini, puno jače.
Kako tanjena sredina čini žbicu jačom? Tako što je čin ielastičnijom, na tom srednjem delu, pa rasterećuje krajeve žbica, koji su inače pod većim stresom i obično oni pucaju. Zato su ove tanjene žbice (2 mm na krajevima, a 1,8 mm na sredini) jače od onih koje su istog prečnika celom dužinom. Jeste malo kontraintuitivno, ali tako je. Treba još napomenuti da se ovo tanjenje radi u fabrici, valjanjem, a ne brušenjem, kako bi se očuvala struktura čelika i kako se ne bi stvorila slaba tačka na kojoj bi žbica pucala.
Vezano za temu prečnika (“debljine”), vredi pomenuti i žbice koje su široke 2,3 mm na laktu, 1,8 mm na sredini, a standardnih 2 mm na delu gde ide nipla (gde su navoji). Poput DT Swiss Alpine III (Amazon affiliate link). Ove žbice su najjače što postoji. Em imaju tanjenu sredinu (što ojačava i one od 2 mm), em su dodatno podebljane na laktu (na 2,3 mm). Jer laktovi su delovi na kojima žbice obično pucaju. Pored toga što je deblji lakat jači sam po sebi, dodatno pomaže što bolje naleže na rupe na nabli – koje se prave da budu previše široke danas – po 2,6 mm najčešće. Što sprečava “obične” žbice širine 2 mm da lepo, “tesno” nalegnu.
Kod žbica, još jedan važan atribut je njihova dužina, ali o tome malo kasnije.
Lično sam imao odlična iskustva sa Sapim i DT Swiss žbicama (Amazon affiliate linkovi).
Napomena: Savremene žbice većine proizvođača prave se sa uglom od 90 stepeni, ili tupljim (95 stepeni i sl.).
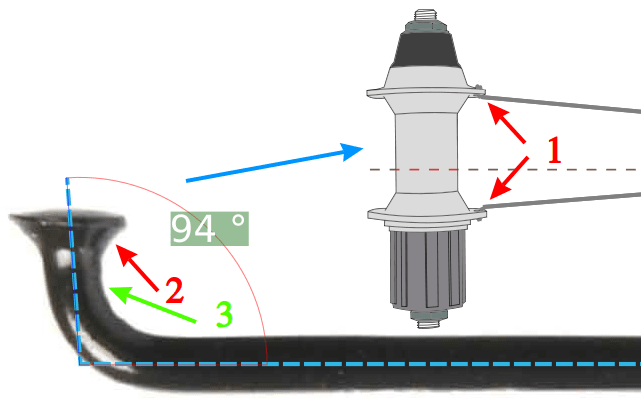
Ležanje žbica u nabli (1), glava žbice (2), i krivina lakta žbice (3)
Slika 5
Na slici 5 je prikazana žbica sa uglom glave od 94 stepena. Ovakav dizajn ubrzava pletenje, a pomaže i žbicama da bolje nalegnu ako je rupa na nabli prevelikog prečnika (što je često slučaj). Sapim pravi ugao od 95 stepeni, dok DT Swiss koristi 90 stepeni.
2.4. Niple
Niple treba da odgovaraju žbicama. Žbice od 2 mm na kraju sa navojima, tražiće i niple za navoj prečnika 2 mm. Ovakve niple će stati i na žbice prečnika 1,8 mm, ali će spoj biti slab i navoji se mogu iskidati pod dejstvom sile zatezanja.
Niple prečnika navoja 1,8 mm, naravno, neće stati na žbice prečnika 2 mm.
Dužina nipli, ako felna ne zahteva drugačije, najbolje da je od 12 mm. Najbrže se prave točkovi i spoj je čvrst i dobar. Postoje i duže niple – od 14 i 16 milimetara.
Napomena: Sapim i DT Swiss prave niple dužine 14 i 16 mm sa dužim navojem. Ovo je loš dizajn. Zašto? Dužina navoja na žbici obično ide do nekih 10 mm. Ako niple imaju duži navoj, žbice neće moći da prođu do kraja niple.

Izvor: Professional Guide to Wheel Building, Roger Musson
Slika 6
Dve leve niple na slici 6 (16 i 14 mm dužine) ne mogu se zavrnuti tako da žbica dođe do kraja. Ne bez da telo žbice (bez navoja) ošteti donje navoje niple i drastično oteža zavrtanje. Ako se ostave ovako, unutrašnji deo vrha niple ostaje šupalj, bez žbice da ga podržava, pa se može odlomiti u vožnji. Sa time sam imao iskustva: problem sa Sapim i DT Swiss niplama dužine 14 i 16 mm.
Što se materijala tiče, postoje aluminijumske i mesingane. Aluminijumske su nešto lakše, ali su manje jake i podložnije su galvanskoj koroziji (članak sa Vikipedije), pa ih radije izbegavam.
3. Način šniranja (pletenja) žbica
U ovom videu sam (na 2 minuta i 48 sekundi), na engleskom, objasnio načine pletenja žbica (link bi trebalo da otvori YouTube snimak na 2:48). Ali ovde je objašnjenje u tekstualnom formatu.
Egzotiku na stranu, postoje dva načina pletenja točkova bicikala: radijalno, i ukršteno. Pre detaljnijeg objašnjenja, par slika koje govore više od reči:

Slika 7
Kod radijalno pletenih točkova, žbice idu od nable direktno do najbliže rupe za žbice na felni.

Slika 8
Kod ukršetno pletenih točkova, žbice idu pod određenim uglom do rupe za žbice na felni, ukrštajući se sa drugim žbicama. Broj ukrštanja može biti veći, ili manji, o tome više kasnije, ali naš točak ima 4 ukrštanja.

Slika 9
Kada broje ukrštanja na točku, ljudima često promakne prvo ukrštanje, sa žbicom koja je odmah susedna (obojena plavom bojom na slici 9).
Ako je sve ostalo identično, ukršteno pleteni točak može podneti puno više opterećenja od radijalno pletenog. Radijalno pleteni točkovi praktično služe samo zbog izgleda (i minimalne uštede u masi, zbog nešto kraćih žbica). Objasniću i zašto.
Video u kojem (na srpskohrvatskom) objašnjavam i demonstriram pletenje točka bicikla:
3.1. Kako ukršteno pleteni točkovi prenose opterećenje
Postoje dve vrste sila. Jetda je u osi točka, kada se pod silom pedalanja nabla pokušava rotirati, oko svoje osovine, u odnosu na felnu – ili, u slučaju kočenja disk kočnicom, kada se felna pokušava rotirati u odnosu na nablu.
Slika 10 pokazuje primer dejstva sile pedalanja – točak je slikan sa leve strane. Kod kočenja disk kočnicom, sila deluje u suprotnom smeru, preko uticaja kojim tlo “gura” felnu prilikom kočenja.

Slika 10
Žbice koje su vučene (na engleskom “trailing”) se zatežu, dok se vodeće (eng. “leading”), šnirane u suprotnom smeru olabavljuju.
Deo gde se vučene i vodeće žbice ukrštaju, je mesto gde dodatno zategnuta vučena žbica jače pritiska vodeću žbicu, čime se smanjuje količina labavljenja vodeće žbice. Ovo je jedna od prednosti ukrštenog šniranja.
Druga sila koja deluje je bočni pritisak na felnu, u odnosu na nablu.

Slika 11
Na primeru sa slike 11, zamislimo da sila deluje sa desne strane felne, u smeru od gledaoca, ka tim plavim vratima. U tom slučaju, žbice koje su bliže nama, na mestu blizu tačke delovanja sile, će se zatezati (pošto felna “beži” od njih). One dalje od gledaoca, bliže vratima, će se labaviti.
Zbog ovakvih sila, žbice se pletu pod uglom u odnosu na nablu, kako bi se nabla koristila u funkciji poluge.

Slika 12
Što je žbica pod većim uglom (tj. što ima više ukrštanja), to će poluga biti veća i točak će lakše podnositi lateralne pritiske. Zamislite da crvena žbica sa slike 12 ide skroz preko glave susedne žbice (obojene plavom bojom i označene crvenom strelicom). To bi činilo polugu još dužom. Međutim, tada bi bilo teško zameniti puknutu žbicu (jer je pristup blokiran). Takođe, glava žbice bi krivila žbicu koja prelazi preko nje, čime bi se ta žbica slabila. Zato je važno birati optimalan broj ukrštanja. Slika 12 prikazuje malo preklapanja – na granici prihvatljivog.
3.2. Optimalan broj ukrštanja
Broj ukrštanja treba da je toliki da se dobije najveći mogući ugao žbice u odnosu na nablu, ali do granice da žbica ne prelazi preko glave susedne žbice.
Tačan broj ukrštanja kojim se ovo postiže u najvećoj meri zavisi od ukupnog broja žbica (i, u manjoj meri, od prečnika nable i felne). Na koji način?
Točak sa 36 žbica ima ugao između svake rupe od po 10 stepeni (360/36). Svaka rupa na nabli, sa svake strane, je na duplo većem uglu od susedne rupe (pošto pola žbica ide sa jedne strane nable, a pola sa druge).
Ako je točak sa 20 žbica, tj. ima svega 20 rupa na felni, rupe se nalaze na po 18 stepeni na felni, odnosno na po 36 stepeni na nabli.
Žbice idu u grupama od po 4:

Slika 13
Uvek idu po dve, gotovo paralelne vodeće (ili vučene), po jedna sa svake strane nable.
Zatim dve vučene (ili vodeće), po jedna sa svake strane nable.
I tako u krug. Koliko god da ima žbica i sa kolikim god brojem ukrštanja da se pravi točak – ove grupe od po 4 žbice su uvek prisutne.
Ukrštene žbice su 1 i 3, kao i 2 i 4.
Da bi se izračunao ugao žbica, treba pomnožiti ugao rupa na nabli sa brojem ukrštanja. Kod točka sa 36 žbica, to bi bilo 20 stepeni puta broj ukrštanja.
Ali kako znati kada je ugao prevelik i kada će doći do preklapanja? U praksi, za većinu nabli i felni, ugao do 75 stepeni ne dovodi do preklapanja.
Jednostavan, praktičan način za utvrđivanje optimalnog broja ukrštanja:
podelite broj žbica sa 9 i zaokružite na prvi manji ceo broj (odbacite decimale).
Izuzeci su točkovi sa 36 žbica, gde sa 4 ukrštanja (36/9) često dolazi do manjeg preklapanja (kao što se vidi na slici 12). I točkovi sa 16 žbica, gde se može proći i sa 2 unakrst (jer su rupe za žbice na nabli pod velikim uglom i razmakom).
Radi olakšavanja posla, evo i tabele:
| Broj žbica | Optimalan broj ukrštanja |
| 16 | 1 x (2 x nekad) |
| 20 | 2 x |
| 24 | 2 x |
| 28 | 3 x |
| 32 | 3 x |
| 36 | 3 x (4 x nekad) |
| 40 | 4 x |
| 48 | 4 x |
Tabela 1
3.3. Kako radijalno pleteni točkovi prenose opterećenje
Loše, nikako!
Kod radijalno pletenih točkova, dolazi do (okom neprimetnog) uvijanja nable, te dobijanja loše kopije ukrštenog pletenja radi prenošenja sila. Na slici ispod sam nacrtao položaj žbica, kada se istegnu i zarotiraju (u smeru koji zavisi od smera delovanja sile). Prenaglašeno je da bi se objasnila poenta (i nisam nacrtao pomeraj felne, koja se kreće sa žbicama, naravno).

Slika 14
Tu ima dosta uvijanja i frikcije koji mogu pokidati žbice. Zato se ovako pletu samo prednji točkovi, na biciklima koji ne koriste disk kočnice (i leva strana nekih egzotičnih zadnjih točkova).
Druga mana ovog načina pletenja je što previše napreže nablu – žbice nastoje da je iskidaju. Pogledajte na slici ispod kako tenzija žbica kod unakrst pletenog točka praktično sabija materijal nable, dok ga tenzija radijalno pletenog točka pokušava razvući ka spolja, iskidati:

Slika 15
Video objašnjenje zašto se točkovi pletu i prave ovako kako preporučujem:
4. Značaj izbora optimalne dužine žbica
Idealno je da žbice budu takve dužine da cela dužina navoja niple bude iskorištena za nošenje opterećenja. Uz to, predugačke žbice mogu probušiti gumu na felnama koje nisu duplozidne, ako štrče previše. Isekao sam jednu niplu na pola kako bih ovo demonstrirao. Obeležio sam početak i kraj navoja niple i žbice, pošto se ne vidi jasno na svim slikama.

Slika 16

Slika 17
5. Računanje optimalne dužine žbica
Da bi se izračunala optimalna dužina žbica, potrebno je utvrditi (izmeriti) sledeće sledeće:
- Efektivni prečnik felne (ERD – eng. Effective Rim Diameter) i druge važne dimenzije felne.
- Važne dimenzije nable (prečnik i slično).
- Prečnik (debljina) žbica koje se koriste (tanje se više izdužuju pri zatezanju).
- Broj žbica i broj ukrštanja.
Broj žbica i ukrštanja sam objasnio u ovom članku, dok ću za ostale pojmove stavljati linkove kako koji članak napišem i dopunim.
Uglavnom, na kraju je sve mere najbolje uneti u kalkulator dužine žbica (link je ka kalkulatoru koji najviše koristim).
Video u kojem pokazujem i objašnjavam računanje optimalne dužine žbica:
6. Značaj ujednačenosti tenzije žbica
Kada su žbice neujednačene tenzije, tj. ako su neke labavije, a druge zategnutije, šta se dešava?
- Zategnutije žbice će nositi više opterećenja od labavih, pa će biti više opterećene, a i spoj tih žbica sa nablom i felnom će biti više opterećen.
- Labavije žbice će se, kako se točak okreće, dodatno labaviti kada su na dnu (pri svakom okretu točka), ili kada je točak opterećen tako da im se tenzija smanjuje (npr. bočno opterećenje sa suprotne strane), pa će, pošto su labavije, više da se uvijaju i brže će pući na laktu usled zamora materijala.
Kod zadnjih nabli, kao i kod prednjih ako je točak sa disk kočnicom, postoji jedna začkoljica:
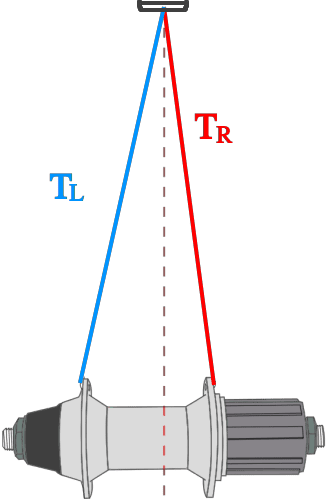
Slika 18
Desne žbice, kod gore pomenutih nabli, zbog oštrijeg ugla, imaju višu tenziju od levih (kako bi felna ostala u osi, tj. u centru). Međutim, tenzija desnih žbica treba da bude što je moguće više ujednačena, u poređenju sa ostalim žbicama na istoj strani (desnoj). Isto važi i za žbice sa leve strane – međusobno treba da imaju što više ujednačenu tenziju.
Kada se pravi točak, ako morate izabrati između 100% prave felne i ujednačenije tenzije žbica, birajte ujednačenu tenziju. Takav točak neće biti 100% prav od starta, ali će ostati takav i posle 20.000 kilometara vožnje (osim ako se felna pokrivi o neku stenčugu). Sa druge strane, ako se točak napravi da bude 100% prav, ali sa nedovoljno ujednačenom tenzijom žbica, vrlo brzo će početi dobijati osmicu, a veća je i verovatnoća da će žbice pucati.
Uz još jednu začkoljicu: točak treba da je prav u granicama prihvatljivih tolerancija, o čemu pišem u narednom poglavlju. To jest, ni 100% ujednačena tenzija žbica nije dobro rešenje, ako je felna tada previše kriva.
Kako meriti i upoređivati tenziju žbica?
Trzalicom za gitaru se mogu okidati, pa po ujednačenosti zvuka dosta precizno oceniti ujednačenost tenzije, poput okitanja struna na gitari.
Meni je puno brže koristiti tenziometar za žbice. Nisam neki sluhista, a i okidanje ne daje podatak o količini tenzije, što je isto važno (70 kiloponda je minimum za većinu točkova). Većina tenziometara nisu dovoljno precizni. Izuzetak je ovaj patent (dizajn pokojnog Jobst Brandt-a), koji prodaje Wheel Fanatyk. I budžet varijanta koju pravi brat Makedonac, Filip Kralyevski – tenziometar.
7. Prihvatljive tolerancije pri pravljenju točka bicikla
Ništa na ovom svetu nije savršeno i idealno, čak ni točkovi bicikla (oni su samo najbliže što se može doći do savršenstva 🙂 ). Mehaničke stvari se obično rade u granicama prihvatljivih tolerancija. Koje su tolerancije kod točkova bicikala, tj. kada se točak smatra zadovoljavajuće pravim i dobro napravljenim?
Definisaćemo prvo pojmove “radijalna centriranost“, “lateralna centriranost“, “poravnatost felne” a “tenzija žbica” je već objašnjena u prethodnom poglavlju.
7.1. Radijalna centriranost
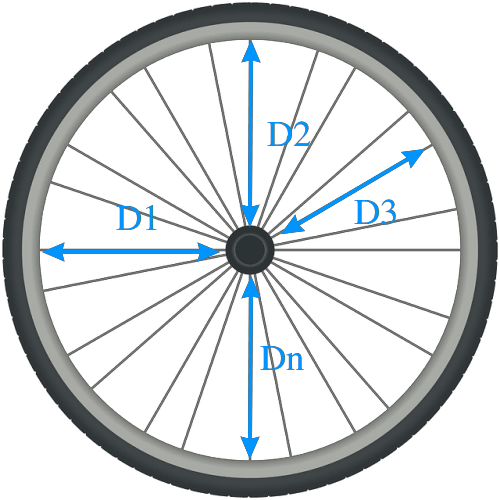
Slika 19
Rastojanja felne od centra točka treba da budu što ujednačenija, duž celog obima točka. Idealno:
D1 = D2 = D3 = … = Dn
Naravno neće biti idealno, ali važno je da se radi u okviru prihvatljivih tolerancija (definisane u poglavlju 7.4).
Video u kojem objašnjavam kako se proverava radijalna centriranost točka.
Dok ne steknete osećaj za vizuelno određivanje veličine zazora, možete se poslužiti ovakvim alatom (Amazon affiliate link).

Klik na sliku za kupovinu na Amazonu (affiliate link)
Slika 20
7.2. Lateralna centriranost
Lateralna (ne)centriranost je ono što svi najlakše prvo primetimo – koliko točak “pravi osmicu”.

Slika 21
I ovde se za merenje odstupanja mogu koristiti gore prikazani “špijuni” – barem dok se ne stekne osećaj.
7.3. Poravnatost felne
U ovom slučaju slika 22 govori više od 1000 reči:
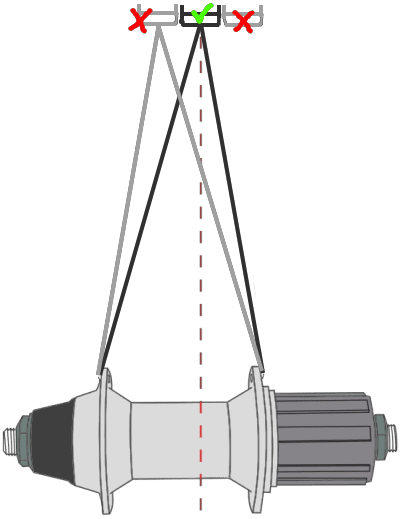
Slika 22
Meri se pomoću alata za merenje poravnatosti felne (amazon affiliate link).

Meri se rastojanje locknut-a (videti objašnjenje OLD na ovom linku) točka sa svake strane, pa upoređuje da li je jednako
Slika 23
Začkoljice postoje kod ovoga – za “egzotične” felne i ramove, videti na ovom linku objašnjenje šta raditi u slučaju asimetričnih felni i offset ramova.
7.4. Prihvatljive tolerancije centriranosti, i ujednačenosti tenzije žbica
Ukratko, spisak prihvatljivih tolerancija za gore objašnjene parametre:
- Ujednačenost tenzije žbica (sa iste strane): odstupanje do +- 10 % tenzije jednih u odnosu na druge (sa iste strane) – idealno +- 5%, tj. da najveće odstupanje između najlabavije i najzategnutije tada bude do 10%.
- Radijalna centriranost: do +- 0,5 mm.
- Lateralna centriranost: do +- 0,25 mm.
- Poravnatost felne: do +- 0,5 mm (merač uvek pokazuje grešku duplirano!).
8. Izvori – toplo preporučeni
- Jobst Brandt – The Bicycle Wheel (Amazon affiliate link)
- Sheldon Brown – Wheelbuilding
- Roger Musson – Professional Guide to Wheel Building
- Moja serija videa o pravljenju točkova. Od tih, možda je najbolje krenut od snimka o zameni nable i pletenju točka (za ostale detalje i procedure videti onda ostale snimke iz serije), pa nastaviti sa videom o tome kako se centrira točak bicikla.
- Moja serija snimaka na engleskom, koja prikazuje kompletan proces pravljenja točka bicikla.
Postojeći komentari (pitanja i odgovori) postavljeni ispod ovog članka, premešteni su u ovu temu BikeGremlin foruma:
https://www.bikegremlin.net/threads/osnove-pravljenja-tockova-bicikala-komentari-clanka.172/


Da, da! Greška u kucanju. U svakom slučaju razumeli smo se.
Hvala
Veliki pozdrav
Norbert
Ćao Norberte,
Bio sam radoznao, pogledao sam u novom izdanju uputstvo za novi kalkulator.
U suštini je isto računanje kao u poslednjoj izmeni. Dakle:
Navrne se nipla do kraja na žbicu (koja se koristi za merenje) dokle ide bez da se baš sili (tj. da navoj niple dođe do dela žbice bez navoja). Onda se odvrne za 5,5 krugova (dakle, neka 2 mm – tj. mislim da je 5,33 kruga tačno 2 mm ali morao bih proveriti). Pa se tako izmeri i unese u kalkulator. Onda bi trebalo da da rezultat koji ostavlja prostora za korekciju ako su žbice malo duže (tj. ako se zaokruži na više).
Da, ovo je adresa nove verzije kalkulatora (moram ažurirati link u članku – lični podsetnik):
https://www.spokelength-project.com/calculator/
Kako se vidi na ovoj slici, kod DT Swiss nipli, kad se izvrnu za tih ~2mm, žbica stoji u liniji sa onim ravnim delom žbice, kako je i bilo preporučeno u prvoj verziji kalkulatora (sa Sapim niplama to ne bude slučaj):

Tako autor piše. Ali u praksi, barem sa tenzijama koje ja koristim (oko 100 kiloponda, kako i autor preporučuju), tako izračunate dužine žbica meni često ispadnu za nijansu predugačke. Moguće da je do nižeg kvaliteta Krypton felni (koje najčešće koristim), ili žbica (planiram do zime preći na Sapim i DT Swiss žbice isključivo – DT Swiss standardne 12mm mesingane niple već koristim). Uglavnom, obično zaokružim na najbliži parni broj (pa i na kraći ako je to bliže) – i tako mi najčešće ispadne optimalna dužina. Ali, da se ogradim, tehnički, školski, trebalo bi zaokruživati na veći.
Nadam se da sam više pojasnio nego što sam zbunio. 🙂
Relja
Relja,
Hvala na bogatim informacijama, kao i na celom sajtu. Mnogo toga sam saznao, a evo i ova tematika mi je mnogo jasnija nego što je bila. Nije problem kad čovek nešto ne zna, tada može da pita. Problem je kad misli da zna, a ispostavi se da ne zna, kao ja kod prvog posta. Bio sam ubeđen da sam na dobrom putu.????
Pozdrav
Norbert
U osnovnoj školi je na zidu hodnika stajao natpis: “Nije sramota ne znati, sramota je ne želeti naučiti.”
Nezgodna stvar kad čovek uči sam, samouk, što se kaže (i učenje preko Interneta u velikoj meri jeste to), je što se puno teže prepozna kad nešto pogrešno razume.
Evo primera (na engleskom) gde sam, pre koji dan, postavio početničko pitanje, pošto sam svestan da je sasvim moguće da to nisam dobro razumeo (ispostavilo se da sam “ubo,” ali mogao sam i omašiti, vrlo lako):
https://www.bikeforums.net/bicycle-mechanics/1273353-odourless-mineral-spirits-german-amazon.html
Relja Još-Uvek-Glup Novović 🙂